Среднее арифметическое: что это такое и как его рассчитать

Среднее арифметическое — это статистический показатель. Школьник с его помощью вычислит свой средний балл по предмету, а работник узнает, какова его средняя зарплата. Нужно применить простую формулу.

Понятие о среднем арифметическом, его применение

В повседневной жизни приходится анализировать значительное количество данных в случаях, когда надо определить среднюю цену товара в разных магазинах, среднесуточную температуру, средний балл успеваемости или среднюю посещаемость занятий и еще во множестве случаев.

Что такое среднее арифметическое? В математике существует несколько определений для этого понятия. Среднее арифметическое — это:

• доля от деления суммы чисел на их количество;
• отношение суммы величин к их количеству;
• сумма всех чисел, деленная на их количество.

Из определений следует, что это показатель для анализа числовых данных, который дает представление о центральных значениях в каком-то наборе чисел. Большим количеством чисел оперирует математика, статистика, когда важно определить средние показатели, например средний доход, средний возраст, среднюю зарплату в отрасли или на предприятии.

Вычисление среднего арифметического — один из основных инструментов статистики, для которой это самый простой и распространенный показатель. Этот способ позволяет оперировать большими объемами чисел без необходимости повторять их снова и снова, достаточно определить их средний показатель.

Среднее арифметическое имеет такие особенности:

• Учитывает каждое число, присваивает каждому из них равную значимость.
• Суммирует все значения, включая экстремальные, выбивающиеся из общего ряда чисел. Это бывает необходимо, когда надо получить представление о всех средних значениях без исключения.
• Помогает описать множество цифровых значений всего одним числом, когда надо сжато изложить информацию или описать множество измерений.
• Усредняет множество значений. Это похоже на процесс «сглаживания» чисел, как отмечается на сайте занимательной математики Math is Fun.

Метод вычисления среднего арифметического хорош для данных, которые имеют нормальное распределение, которых много и они не очень сильно отличаются одно от другого. Но наряду с сильными сторонами, этот способ имеет и некоторые недостатки:

• Он чувствителен к так называемым выбросам, когда в наборе чисел есть значительные отклонения, сильно меняющие результат.
• Вычисление среднего арифметического неуместно для неравномерных данных, когда в наборе чисел есть значительные различия. Они дают искаженную картину среднего значения. Например, если считать среднее арифметическое между числами 2 и 1000 получится 501, что трудно принять как средний показатель этих чисел.

При вычислении среднего арифметического следует учитывать его особенности. Если данные для анализа будут им соответствовать, тогда средний показатель будет отражать реальную картину.

Как рассчитать среднее арифметическое

Как найти среднее арифметическое? При его вычислении выполняются два арифметических действия: сначала надо сложить все необходимые числа, затем разделить полученную сумму на количество слагаемых чисел. На сайте издателя образовательных ресурсов Twinkl это выражено так: среднее арифметическое=общая сумма всех чисел÷количество чисел.

При вычислениях среднее арифметическое обозначается греческой буквой μ (Ми). Слагаемые числа можно обозначить как ч₁, ч₂, ч₃…чₙ, а их количество буквой N. По какой формуле вычислить среднее арифметическое? Формула была выведена такая: μ=(ч₁+ч₂+ч₃…+чₙ)÷N. Например, если надо рассчитать среднее арифметическое набора из четырех чисел 2, 4, 6, 8, то это будет выглядеть так: μ=(2+4+6+8)÷4=20÷4=5, то есть среднее арифметическое указанного набора чисел равно 5.

В начальных и старших классах уровень сложности задач на вычисление среднего арифметического сильно отличается.

Вычисление среднего арифметического в начальных классах

Ученику интересно самому рассчитать свою среднюю оценку по предмету за четверть. По принятой в Казахстане 10-балльной шкале он получил за это время за устные ответы оценки 9, 7, 10, за самостоятельные работы — 7, 8, за контрольную — 9 (всего 6 оценок). Средняя оценка будет равна сумме всех баллов, деленной на их количество: (9+7+10+7+8+9)÷6=50÷6=8,33. Средний балл по предмету — 8,3 (при округлении — 8).

Вычисление среднего арифметического в средних классах

Более сложные задачи по вычислению среднего арифметического в основной школе бывают с подвохом. Например, дано среднее арифметическое четырех чисел, оно равно 3,4. Среднее арифметическое шести других чисел равно 8,3. Надо найти среднее арифметическое этих 10 чисел.

Просто сложить указанные средние показатели и разделить на 2 будет неправильно, потому что в условиях идет речь о 10 числах. Надо вспомнить, что в среднем арифметическом применяется сумма чисел. Поэтому решение должно быть таким:

1. Сначала найдем сумму четырех чисел. Для этого их средний показатель умножим на 4: 3,4×4=13,6.
2. Затем найдем сумму 6 чисел: 8,3×6=49,8.
3. Складываем полученные суммы и узнаем сумму 10 чисел: 13,6+49,8=63,4.

Теперь легко найти среднее арифметическое 10 чисел. Надо их сумму разделить на 10: 63,4÷10=6,34. Для правильного решения такой задачи придется применить не только сложение и деление, как для вычисления простого среднего арифметического, но и другие действия.

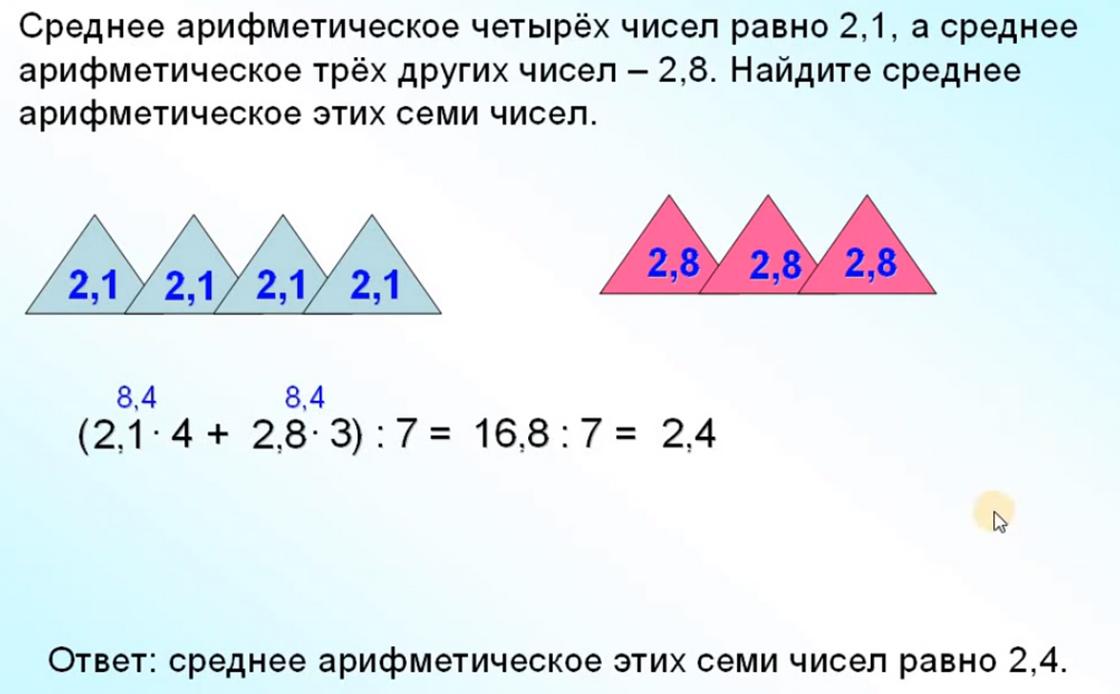
Как найти среднее арифметическое дробных чисел

Задачи на вычисление среднего арифметического дробных чисел только на первый взгляд кажутся сложными. На самом деле при этом выполняют такие же вычисления, как с целыми числами, но более громоздкие. Например, надо найти среднее значение чисел 5,24, 6,97, 8,56, 7,32, 6,23. Сначала следует сложить эти дроби: 5,24+6,97+8,56+7,32+6,23=34,32. Дальше эту сумму разделить на количество дробей, то есть на 5: 34,32÷5=6,864. Это и будет средний показатель набора дробных чисел.

Найти среднее арифметическое можно из любого набора чисел. Такой навык пригодится на многих экзаменах и в разных ситуациях повседневной жизни.