Сокращение дробей: в каких случаях выполняется и как сделать правильно

Математика — наука, которая стремится к точным, кратким и красивым выражениям. При этом выполняется негласное правило сокращать все, что сокращается. Оно применяется и к дробным числам.

Сокращение дробей приводит к их упрощению. С простыми числами математические действия выполняются быстрее.

Что надо знать о сокращении дробей

Что такое сокращение дробей? Это замена дроби с большими числами на равную ей с меньшими числами, что можно выполнить при соблюдении определенных правил. Главное при сокращении дроби — разделить ее числитель и знаменатель на их общий делитель, то есть на одно и то же число. Это число должно быть положительным, не равным 0 или 1.

В результате деления получим новую дробь с другими числами. Но она будет равна исходной, потому что отвечает основному свойству дробей, которое звучит так: если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной. Математически это свойство выражается так: a/b=a×m/b×m или a/b=a:m/b:m, где a, b, m — натуральные числа.

Обычно эти действия записываются так: например, в дроби 8/36 числитель и знаменатель делятся на 4, но само действие выполняется устно и не записывается. Числа зачеркиваются и рядом вверху около каждого пишется результат деления, затем полученный результат сокращения дроби — 2/9.

Смысл сокращения дроби заключается в том, что в результате числитель и знаменатель оказываются наименьшими из возможных чисел. Цель сокращения дроби — получение несократимой дроби, когда и числитель и знаменатель становятся взаимно простыми числами.

При сокращении дробей с небольшими числами достаточно устно определить общий делитель, опираясь на таблицу умножения. Например, в дроби 15/25 числитель и знаменатель делятся на 5, после сокращения получается 15/25=3/5. Числа 3 и 5 простые, то есть делятся только на себя и на 1.

В дробях с большими числами надо вспомнить способ разложения числа на простые множители. Это выполняют в столбик, где слева от вертикальной черты пишется число, за чертой — самый наименьший делитель (если число четное — деление начинают с 2). Это действие повторяется, пока в результате не останется 1.

При этом следует разложить на простые множители сначала числитель, затем знаменатель. Затем выбирается наибольший общий делитель (НОД) — наибольшее число, на которое и числитель, и знаменатель делятся без остатка. Находят НОД, как подсказывает математический онлайн-сервис Match Planet, как произведение общих множителей.

Эти действия по сокращению дроби сводятся к общему правилу. Как сделать сокращение дробей? Действие выполняют в такой последовательности:

1. Сначала надо найти наибольший общий делитель (НОД) числителя и знаменателя.
2. Затем разделить числитель и знаменатель на НОД, чтобы получить несократимую дробь.

Умение сокращать дроби часто применяется в математике. На сайте крупнейшего в мире издателя образовательных ресурсов Twinkl подчеркивают, что в дробях нужна самая простая их форма. Это позволит легко делать любые вычисления, при которых требуется складывать, вычитать, делить или умножать дробные числа.

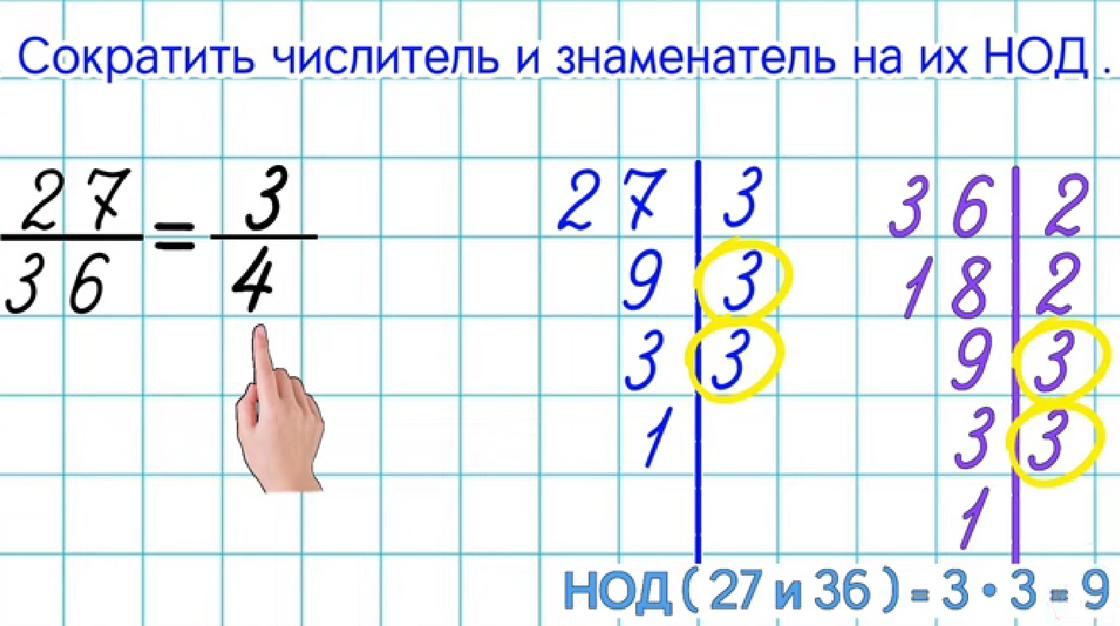
Способы сокращения дробей

При сокращении разных дробей придется пользоваться разными алгоритмами. При этом правило остается общим, а способы определения общего делителя отличаются. Важно научиться быстро определять НОД с помощью таблицы умножения или раскладывая число на простые множители. Можно при этом воспользоваться онлайн-калькулятором, но лучше делать самостоятельно, чтобы вырабатывать необходимые навыки.

Алгоритм последовательного сокращения дробей

Простой способ сокращения дробей — последовательное сокращение числителя и знаменателя. Этот способ применяется, если оба числа четные или если это крупные числа и трудно сразу подобрать НОД.

Пример 1. Сократим дробь 48/64. Видим, что числитель и знаменатель — четные числа, их можно последовательно делить на 2: 48/64=24/32=12/16=6/8=3/4. Ответ: 48/64=3/4.

Пример 2. Сократить дробь 150/225. В этой дроби числитель и знаменатель — нечетные числа, делим их на 3: 150/225=50/75. В полученной дроби обе части можно разделить на 5: 50/75=10/15. Еще можно разделить оба числа на 5: 10/5=2/3. Получили неделимую дробь. Ответ: 150/225=2/3.

Пример 3. Сократить дробь 2000/4400. В ней можно разделить оба числа сначала на 100, потом дважды на 2 или сразу на 4: 2000/4400=20/44=10/22= 5/11. Ответ: 2000/4400=5/11.

Алгоритм разложения числителя и знаменателя на множители

Способ применяют при сокращении дробей с большими числами, когда сразу трудно найти НОД. При этом числитель и знаменатель следует разложить на простые множители отдельно. Затем, как подсказывает онлайн-сервис Match Planet, общие множители надо перемножить, а остальные мысленно убрать.

Пример: надо сократить дробь 420/2520. Раскладываем на простые множители числитель и знаменатель: 420=2×2×3×5×7; 2520=2×2×2×3×3×5×7. Выбираем общие множители и перемножаем: 2×2×3×5×7=420. Полученное число будет НОД. Теперь делим на него числитель и знаменатель: 420/420=1; 2520/420=6. Ответ: 420/2520=1/6.

Как сокращать смешанные дроби?

Смешанные дроби состоят из целого и дробного числа. Сокращать их можно двумя способами:

1. Платформа Twinkl указывает, что смешанную дробь следует сначала преобразовать в неправильную, а затем сокращать ее по тем же шагам, что и обычную дробь. Смешанную дробь в неправильную преобразуют так: целое число надо умножить на знаменатель и к полученному числу прибавить числитель. Полученное число записать как числитель, а знаменатель не меняется.
2. Одна из ведущих платформ для изучения математики Cue Math предлагает смешанную дробь сокращать иначе: целое число оставить неизменным, а дробную часть сокращать по правилам правильной дроби.

Это самые простые способы сокращения дробей. В старших классах изучают более сложные формулы и методы.

Сокращение дробей позволяет делать вычисления быстрее, не путаясь в огромных числах. Навыки упрощения дробей совершенствуются с каждым решенным примером.